之前环球教育梁永文老师介绍完在处理加减法的uncertainty的方法以及需要注意的地方，那么这一章继续介绍uncertainty的其他情况。

　　考试之中所给的式子有些时候就不是加减的，而是乘除，那么处理乘除的uncertainty的方法也会不一样。例如: X=AB or X=A/B. A和B都是已经知道他们的误差ΔA和ΔB，需要去计算X的误差，这个时候X的误差计算方式如下：

　　很多学生可能不理解为什么要这么去计算，为什么不能像加减的公式一样，直接把absolute uncertainty直接加起来，而是把fractional uncertainty加起来。

　　其实道理很简单，这里举一个例子：通过实验我们推断出T（周期）=L（绳子长度）×M（质量），我们已经知道L和M的absolute uncertainty分别是ΔL和ΔM，而他们的单位分别是m和kg，如果计算T的误差的时候，直接把ΔL和ΔM相加，就意味着单位m和kg相加，这是不合乎规则的，因为两个单位不一样的东西是无法相加的，是没意义的。

　　但如果通过fractional uncertainty来计算，就不一样了，就好象ΔL/L，他们的单位已经被抵消掉，同理M和ΔM的单位也会被抵消，所以他们是可以进行运算的。另外需要注意的是，乘法除法，都是fractional uncertainty相加。

　　除此以外，由于算出来的是fractional uncertainty，考试中是需要学生填写absolute uncertainty的，所以学生需要把算出来的fractional uncertainty乘以real value。

　　在考试中还会出现多次幂的公式，例如：

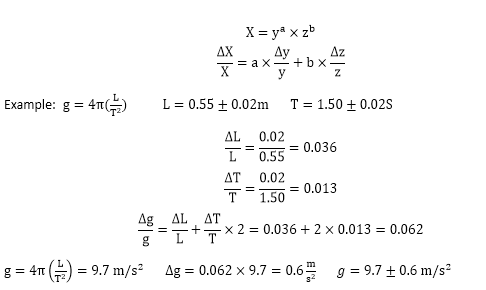
　　需要注意的是，乘法除法都是同样适用的。

　　在考试之中还有可能出现一些比较复杂的情况，例如：

　　遇到这种情况，就不能用上面的办法，因为涉及到log。我们需要用的是求误差最基础最万能的办法：

　　这个求误差的办法，适用于上面所有例子，算出来的答案是一样的。但这种方法比较麻烦而且费时间。需要注意的是，在算最大值，最小值的时候，如何取值要小心。